2,885
2,885
Member
Now....here's the thing....I want someone who knows what they are talking about to decide this....
because I am 100% certain about this
OK, then let's make it $500?
Now....here's the thing....I want someone who knows what they are talking about to decide this....
because I am 100% certain about this
Now....here's the thing....I want someone who knows what they are talking about to decide this....
because I am 100% certain about this
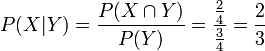
im not going to lose, i am a math type....the problem will be finding someone who knows what the hell they're talking about to settle it...
THANK YOU I WIN....A random two-child family whose older child is a boy is chosen. What is the probability that the younger child is a girl?
 hno:
hno:send it to me...you just proved my case
It seems a review of combinations vs. permutations is in order...
See: http://www.mathsisfun.com/combinatorics/combinations-permutations.html
If order does not matter (which it doesn't in this case) and you have two equal possibilities, then the chance of either of those possibilities being valid is 50%. The other child can be only a boy or a girl, THAT'S IT. They are both as likely to be true.
The line "He does not tell you whether the son is the oldest child or the youngest child." has no influence on the question.
 hno:
hno:thank you....ugh...celtic, now he's gonna call YOU an idiot